Demystifying error-control coding

Many of us have heard the term error-control coding in connection with modern land mobile radio systems, but few of us understand what it is, what it does and why we should be concerned about it. Old timers are forewarned: All LMRs eventually will be digital, and all digital radios use error-control coding. Terms like Golay code, Hamming code, CRC and interleaving will become popular topics at cocktail parties. Don’t get left out of the conversation; learn about error-control codes.

This article begins a series that will examine what error-control codes do, how they work, and when they can be used successfully.

Error-control coding is a discipline under the branch of applied mathematics called Information Theory, discovered by Claude Shannon in 1948 [1]. Prior to this discovery, conventional wisdom said that channel noise prevented error-free communications. Shannon proved otherwise when he showed that channel noise limits the transmission rate, not the error probability.

Shannon showed that every communications channel has a capacity, C (measured in bits per second), and as long as the transmission rate, R (also in bits per second), is less than C, it is possible to design a virtually error-free communications system using error-control codes. Shannon’s contribution was to prove the existence of such codes. He did not tell us how to find them.

After the publication of Shannon’s famous paper, researchers scrambled to find codes that would produce the very small probability of error that he predicted. Progress was disappointing in the 1950s when only a few weak codes were found.

In the 1960s, the field split between the algebraists, who concentrated on a class of codes called block codes, and the probabilists, who were concerned with understanding encoding and decoding as a random process. The probabilists eventually discovered a second class of codes, called convolutional codes, and designed powerful decoders for them.

In the 1970s, the two research paths merged, and several efficient decoding algorithms were developed. With the advent of inexpensive microelectronics, decoders finally became practical and in 1981, the entertainment industry adopted a very powerful error control scheme for the new CD player [2]. Today, error-control coding in its many forms is used in almost every new communications system, including the Association of Public-Safety Communications Officials’ Project 25 standard.

Digital communications systems often are conceptualized as shown in Figure 1. The following paragraphs describe the elements of Figure 1 and define other terms common to error-control coding.

• Encoder and decoder: The encoder adds redundant bits to the sender’s bit stream to create a code word. The decoder uses the redundant bits to detect and/or correct as many bit errors as the particular error-control code will allow. For our purposes, encoding and decoding refers to channel coding as opposed to source coding. (Source coding prepares the original information for transmission; the vocoder, or voice-encoder, is one example of source coding.)

• Modulator and demodulator: The modulator transforms the output of the encoder, which is digital, into a format suitable for the channel, which is usually analog (e.g., a radio channel). The demodulator attempts to recover the correct channel symbol in the presence of noise.

  When the wrong symbol is selected, the decoder tries to correct any errors that result. Some demodulators make soft decisions, meaning that the demodulator does not attempt to match the received signal to one of the allowed symbols. Instead, it matches the noisy sample to a larger set of discrete symbols and sends it to the decoder where the heavy lifting is done.

• Communications channel: This part of the communication system introduces errors. The channel can be radio, twisted wire pair, coaxial cable, fiber-optic cable, magnetic tape, optical discs or any other noisy medium.

• Error-control code: The set of code words used with an encoder and decoder to detect errors, correct errors, or both detect and correct errors.

• Bit-error rate (BER): The probability of bit error often is the figure of merit for an error-control code. We want to keep this number small, typically less than 10-4 for data and less than 10-3 for digital voice. BER is a useful indicator of system performance on an independent error channel, but it has little meaning on bursty, or dependent, error channels.

• Message-error rate: This probability of message error is sometimes called frame error rate. This may be a more appropriate figure of merit because the smart user wants all of his or her messages to be error-free and couldn’t care less about the BER.

• Undetected message error rate (UMER): This is the probability that the error detection decoder fails and an errored message (code word) slips through undetected. This event happens when the error pattern introduced by the channel is such that the transmitted code word is converted into another valid code word. The decoder can’t tell the difference and must conclude that the message is error-free. Practical error detection codes ensure that the UMER is very small, often less than 10^-16.

• Random errors: These errors occur independently. This type of error occurs on channels that are impaired solely by thermal (Gaussian) noise. Independent-error channels also are called memory-less channels because knowledge of previous channel symbols adds nothing to our knowledge of the current channel symbol.

• Burst errors: These errors are not independent. For example, channels with deep fades experience errors that occur in bursts. Because the fades result in consecutive bits that are more likely to be in error, the errors are usually considered dependent rather than independent. In contrast to independent-error channels, burst-error channels have memory.

• Energy per bit: This refers to the amount of energy contained in one information bit. This is not a parameter that can be measured by a meter, but it can be derived from other known parameters. Energy per bit (E_b) is important because almost all channel impairments can be overcome by increasing it. Energy per bit (in joules) is related to transmitter power P_t (in watts and bit rate R (in bits per second), as shown in Equation 1.

  If transmit power is fixed, the energy per bit can be increased by lowering the bit rate. This is why lower bit rates are considered more robust. The required energy per bit to maintain reliable communications can be decreased through error-control coding, as we shall see in the next article in this series.

• Coding gain: This refers to the difference in decibels (dB) in the signal-to-noise ratio required to maintain reliable communications after coding is employed. Signal-to-noise ratio is usually represented as E_b/N₀, where N₀ is the noise power spectral density measured in watts/Hertz (joules). For example, let’s say a communications system requires an E_b/N₀ of 12 dB to maintain a BER of 10^-5, but after coding it requires only 9 dB to maintain the same BER. In that case, the coding gain is 12 dB – 9 dB = 3 dB. (Recall that dB = 10 log10 X, where X is a ratio of powers or energies.)

• Code rate: Consider an encoder that takes k information bits and adds r redundant bits (also called parity bits) for a total of n = k + r bits per code word. The code rate is the fraction k/n, and the code is called an (n, k) error-control code. The added parity bits are a burden (i.e., overhead) to the communications system, so the system designer often chooses a code for its ability to achieve high coding gain with few parity bits.

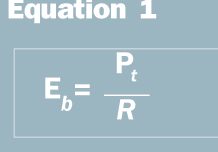
Next month: What coding can and cannot do.

Jay Jacobsmeyer is president of Pericle Communications Co., a consulting engineering firm located in Colorado Springs, Colo. He holds bachelor’s and master’s degrees in Electrical Engineering from Virginia Tech and Cornell University, respectively, and has more than 20 years experience as a radio frequency engineer.

References:

1. C. E. Shannon, “A Mathematical Theory of Communication,” Bell System Technical Journal, vol. 27, pp. 379-423, 1948.

2. F. Guterl, “Compact Disc,” IEEE Spectrum, vol. 25, No. 11, pp. 102-108, 1988.