Listen up–Understanding the decibel

Welcome back class. The holidays are over and it’s time to review. Today’s lesson is the decibel, abbreviated as dB.

To the frustration of police and fire chiefs, radio engineers and technicians speak the foreign language of dBs. Do we enjoy confusing management? Perhaps, but the real reason for using dBs is convenience. It’s easier to add and subtract than to multiply and divide. Decibels allow us to add and subtract. We’ll see shortly why this is true.

First, a little history. The public’s knowledge of decibels is almost exclusively tied to the measure of acoustic energy. The subject comes up when we buy a lawn mower or set noise standards for trucks in urban areas. The decibel’s roots are actually in the telephone industry where it was used to quantify attenuation of audio levels in telephone circuits. Originally, the telephone company measured attenuation indirectly in units of Miles of Standard Cable, where 1 MSC was the loss of power over a 1-mile length of standard cable at a frequency of 795.8 Hz. This was roughly the smallest attenuation detectable to the average listener. In the 1920s, engineers at Bell Labs invented the Transmission Unit (TU) to replace the MSC. The TU was defined as ten times the base-10 logarithm of measured power to a reference power level. Conveniently, the definition was created so that one TU equals approximately one MSC. In 1928, American Telephone and Telegraph (the Bell System) officially renamed the TU the decibel. At the same time, it defined the bel (10 decibels) in honor of its founder, Alexander Graham Bell.

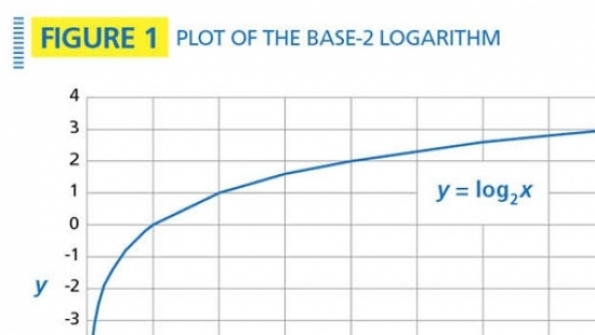
Logarithms and logarithmic identities. Decibels are all about logarithms, so this is a good place to start. The logarithm of a number is the exponent by which another number, called the base, must be raised to produce that number. It is expressed as y = log_b(x) where b is the base. For example log₁₀(100) = 2 because 10² = 100. Natural logarithms use a base equal to the constant e (e = 2.7183…) and they are used widely in mathematics. In information theory, base-2 logarithms are popular. Figure 1 is a plot of the base-2 logarithm. Like all logarithms, the curve approaches an asymptote at x = 0 and is undefined for x < 0. In radio, we are interested almost exclusively in base-10 logarithms. Some useful logarithmic identities:

• log(xy) = log(x) + log(y) because exponents add in a product of two identical bases
• log(x/y) = log(x) – log(y) because exponents subtract in a quotient of two identical bases 
• log_b(x^d) = d log_b(x) because (b^c)^d = b^cd
• log_b(b) = 1
• log_b(1) = 0

We also can change the base of a logarithm:

log_ba = (log_da/log_da)

For example, to change the base from e to 10, we divide the original base e logarithm by log_e(10) = 2.3026.

Decibels. The ratio of two power or energy levels in decibels is defined as 10 times the base-10 logarithm of the ratio of the two power quantities. We can write it as 10 log₁₀(P₁/P₂). The decibel is the logarithm of a ratio, so it is unit-less. If we are interested in decibels relative to a specific reference, such as 1 milliwatt (mW), then the unit is dBm. Other common units are dBW (relative to 1 W) and dBc (relative to the power at the carrier frequency). Sometimes receiver sensitivity is specified in units of dBµV, which is equal to 20 log₁₀(V_s) where V_s is the rms voltage of the minimum useable signal. Similarly, units of dBµV/m sometimes are used when measuring field strength of an over-the-air signal. In this case, the unit is equal to 20 times the base-10 logarithm of the field strength in µV/m.

Thanks to the logarithmic identities presented above, decibels allow us to add and subtract exponents rather than multiply and divide large numbers. Indeed, the ability to deal with very large and very small numbers is really the main advantage of decibels. We would much rather write –118 dBm than 1.6 x 10^–12 mW. Note that ratios less than 1 will result in negative values in decibels.

Once we are familiar with decibels, we can take a lot of shortcuts. The first and most important shortcut is to notice that a factor of 2 equals 3 dB. Every time we double or halve the power, we add or subtract 3 dB. Thus, 1/2 = –3 dB, 1/4 = –6 dB, 1/8 = –9 dB. Table 1 lists some of the common ratios used in the radio field and their decibel equivalents.

Adding power. In radio we don’t always multiply and divide power levels. Sometimes we really want to add powers. When you are accustomed to working in dBs, adding power can throw you for a loop. Algebra is required. Let’s say you are conducting an interference study and want to know what interference power level will cause a 1 dB desense of the receiver. Is it a signal 1 dB above the noise floor? Actually, no. What we want to know is what level of interference, when added to the thermal noise floor in the receiver, causes the total power to be 1 dB greater than the original noise floor. (We are assuming that interference has the same detrimental effect on receiver sensitivity as thermal noise.)

Divide each side of the equation by 10, raise both sides to a power of 10 and do some algebra to get the following:

Mathematically, the relationship is:

10 log₁₀[(x_i + x_n)/x_n] = 1 dB
Where x_i is the interference power and x_n is the noise power in the receiver.

(x_i + x_n)/x_n= 1.26
x_i / x_n + 1 = 1.26
x_i/ x_n = 0.26
which is very close to 1/4 or –6 dB

Thus, the rule of thumb is that signals 6 dB below the thermal noise floor of the receiver, or weaker, will create no more than 1 dB of desense.

Commons mistakes. Following are two examples of the misuse and abuse of decibels:

• The sensitivity of the receiver is –118 dB. No, the sensitivity is the minimum power required for the receiver to produce a useful signal at its output. It is not a unit-less ratio of powers; it is a power. (It also is correct to say that it is a ratio of the received power to 1 mW.) The sensitivity is really –118 dBm.
• The first signal is greater than the second signal by 10 log₁₀ (V₁/V₂) dB. No, decibels are ratios of power, not voltage. It would be correct, however, to write 10 log₁₀ (V₁/V₂)² dB or equivalently, 20 log₁₀ (V₁/V₂) dB.

Homework. To test your understanding of the above, solve the following problems. The answers are at the end of this article.

1. What is the voltage/amplitude ratio equivalent to 12 dB SINAD?
2. To what distance can an existing microwave link be extended so the power drops no more than 3 dB?
3. What is the dynamic range of a 12-bit A/D converter?
4. If Einstein was an engineer and not a physicist, how would he write his famous expression?

Jay Jacobsmeyer, KD0OFB, is president of Pericle Communications, a consulting engineering firm located in Colorado Springs, Colo. He holds bachelor’s and master’s degrees in Electrical Engineering from Virginia Tech and Cornell University, respectively, and has more than 30 years experience as a radio frequency engineer.

Homework answers:

1. Power is proportional to the square of voltage, so the answer is antilog₁₀(12/20) = 4. (The base 10 antilog of x is simply 10 to the x power.)
2. On a line-of-sight microwave link, free space loss is the only path attenuation, and power attenuates proportionately to the square of the distance. In other words, it attenuates 20 dB per decade or equivalently, 6 dB per octave. A 3 dB decrease in power occurs at a relative distance of the square root of 2. So you can extend the link by no more than a factor of 1.414.
3. The 12 bits represent 2¹² discrete voltage (not power) levels. Therefore, the dynamic range is 20 log₁₀ 2¹² = 240 log₁₀ 2 = 72.3 dB.
4. e = mc² +/– 3 dB