What you see is what you get
The Smith chart is a graphical aid for solving transmission line problems. It was created in 1939 by Phillip H. Smith while working at Bell Labs. In this day of personal computers, spreadsheets and smartphones, a graphical solution may seem quaint but the Smith chart is still an essential tool for radio-design engineers. In fact, it is an integral part of computer-aided design (CAD) software and the radio-frequency network analyzer. Perhaps most importantly, thinking in terms of the Smith chart develops intuition about transmission-line and impedance-matching problems.
Preliminaries. Before we jump into the structure of the Smith Chart, let’s recall that impedance is a complex number that consists of a real part (resistance) and an imaginary part (reactance). In general, impedance is written as Z=R+jX, where R is the resistance and X is the reactance. A positive reactance indicates an inductive circuit while a negative reactance indicates a capacitive circuit. When an antenna or other load is connected to a transmission line and a RF signal is generated at the opposite end, the interaction between energy in the line and the load will create reflections on the line. The ratio of voltage to current — which is the definition of impedance — also changes with position on the line. Starting at the load and working backward, the load impedance appears again at a distance of 1/2 wavelength and the cycle repeats.
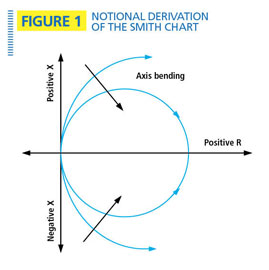
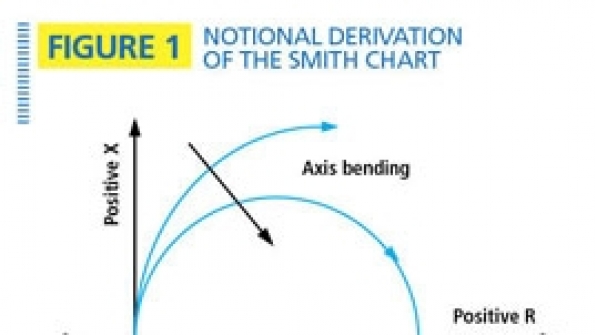
Impedance can be plotted in a rectangular-coordinate system, but the repeating cycle is very messy to represent. This behavior is much better represented on a polar-coordinate system. It helps to think of the problem in the following way: If we start with a rectangular-coordinate system like the one in Figure 1, and distort the reactance axis (y axis) into a number of circles with incrementally larger radii, we now represent constant resistance by a circle rather than a vertical line. Similarly, lines of constant reactance also become arcs, but with their ends at the chart edge.
The Smith chart explained. The Smith chart is used to solve the transmission line impedance equation, where Z0 is the characteristic impedance of the transmission line (usually 50 ohms), ZL is the load impedance, b is the propagation constant of the line, and l is the distance on the line measured from the load. (See Equation 1.) Solving this equation is messy when done manually, but even when a computer is available, the Smith chart is the preferred solution because it aids understanding.

A simplified Smith chart is shown in Figure 2. Resistance is shown on the horizontal axis and lines of constant resistance are represented by circles that cross the horizontal axis and are aligned with the far right side of the chart. Zero resistance appears at the far left side of the horizontal axis and infinite resistance appears at the far right side. The system impedance of 50 ohms is at the center of the chart. (Most Smith Charts are normalized to a system impedance of 1 ohm, but the same principles apply.)
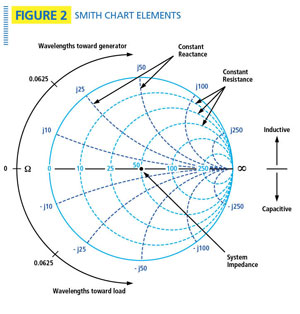
Lines of constant reactance are arcs with one end on the outside circle and the other end at infinity. Reactance above the horizontal axis is positive (inductive) while reactance below the horizontal axis is negative (capacitive). A line of constant standing wave ratio (SWR) is a circle centered at 50 ohms. A SWR of 1.0 is simply a point at the center of the chart, while an SWR of infinity is a circle coinciding with the outside edge of the chart. Moving clockwise is equivalent to moving toward the generator while moving counterclockwise is equivalent to moving toward the load. A complete circle equals 1/2 wavelength, or 180 electrical degrees.
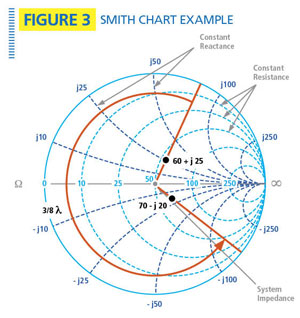
Let’s consider an example: One important use of the Smith chart is to calculate the impedance of the load when the only measurement available is at the end of a transmission line connected to the load. This problem commonly occurs when measuring the impedance of an antenna with a jumper cable permanently attached. Consider the specific case where an antenna comes with an attached coaxial jumper that is 3/8 wavelengths long. Using a network analyzer, we measure the impedance at the jumper’s connector to be Zin=60+j25 ohms. If we rotate this point 3/8 wavelengths counterclockwise (at the same SWR radius), we get a value of ZL = 70– j20 ohms, which is the impedance of the antenna. See Figure 3.
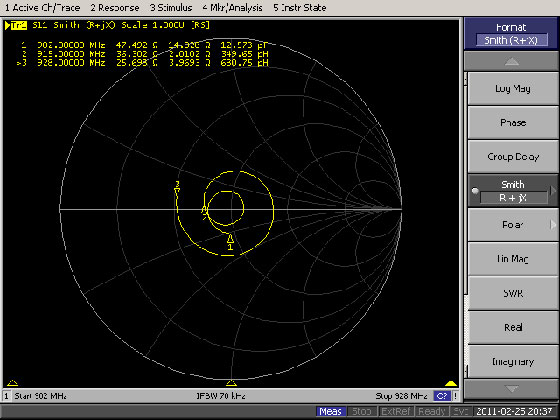
Other uses of the Smith Chart include the design of quarter-wave matching sections, antenna-tuning sections in general and observation of the frequency response of the load. Figure 4 below is an example of a frequency-swept measurement of a 900 MHz dipole antenna using an RF-network analyzer. Note that the antenna has best performance (lowest SWR) at roughly mid-band (915 MHz).
Jay Jacobsmeyer, KD0OFB, is president of Pericle Communications Co., a consulting engineering firm located in Colorado Springs, Colo. He holds bachelor’s and master’s degrees in electrical engineering from Virginia Tech and Cornell University, respectively, and has more than 30 years experience as a radio-frequency engineer.

















This is really good and easy
This is really good and easy understandable book for myself
Thanks and Regards
K D Banerjee/India